Populációdinamika

Az ektoparaziták, azaz külső, a test felszínén élő élősködők (pl. tetű, bolha, atka) a világ számos részén komoly gondokat okoznak napjainkban is. Elterjedésük  gyakran összefüggésben áll a szegénységgel, a rossz higiéniai körülményekkel. Ezek az élősködők számos fertőző betegség – többek között a tífusz és a pestis – terjedéséért is felelősek.Betegséget terjesztő ektoparaziták: ruhatetű, bolha, atka

E betegségek terjedése különbözik például a szúnyogok által terjesztett betegségekétől (malária, nyugat-nílusi vírus stb.), mivel az emberi kapcsolatok hálózatán keresztül terjednek, maguk a betegséget terjesztő ízeltlábúak is betegséghez hasonlóan terjednek.

A jelenséget leíró modellünk újdonsága abban áll, hogy egyszerre modellezi a paraziták és az általuk terjesztett betegségek terjedését. Modellünk legegyszerűbb változatában a populációt három részre osztjuk aszerint, hogy jelen vannak-e az adott részben a paraziták, illetve a betegség. Az egyik rész a fogékonyak csoportja (S), a másodikba azok tartoznak, akik nem fertőző élősködőkkel fertőzöttek (T), a harmadikba pedig azok, akik fertőző élősködőkkel fertőzöttek (Q). A legegyszerűbb modell, amely már eléggé komplex ahhoz, hogy leírja a parazitával és a betegséggel való fertőzés párhuzamos mechanizmusát, a következő nemlineáris differenciálegyenletekkel adható meg: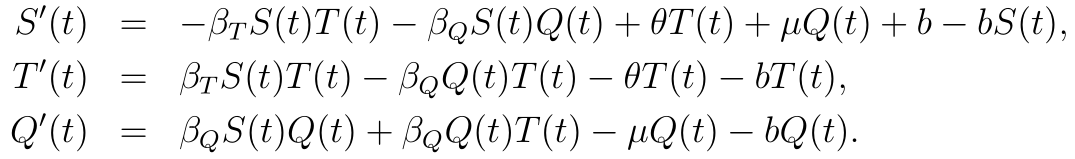A rendszer vizsgálata során kiszámítottuk a rendszer négy egyensúlyi helyzetét, valamint az egyensúlyi helyzetekhez tartozó három reprodukciós számot, és teljes leírást adtunk a megoldások viselkedésére, amely a reprodukciós számoktól függ: három Ljapunov-függvény segítségével beláttuk, hogy minden esetben a négy egyensúlyi helyzet valamelyike globálisan aszimptotikusan stabilis, valamint leírtuk a globális attraktor szerkezetét a reprodukciós számoktól függő öt különböző esetben. 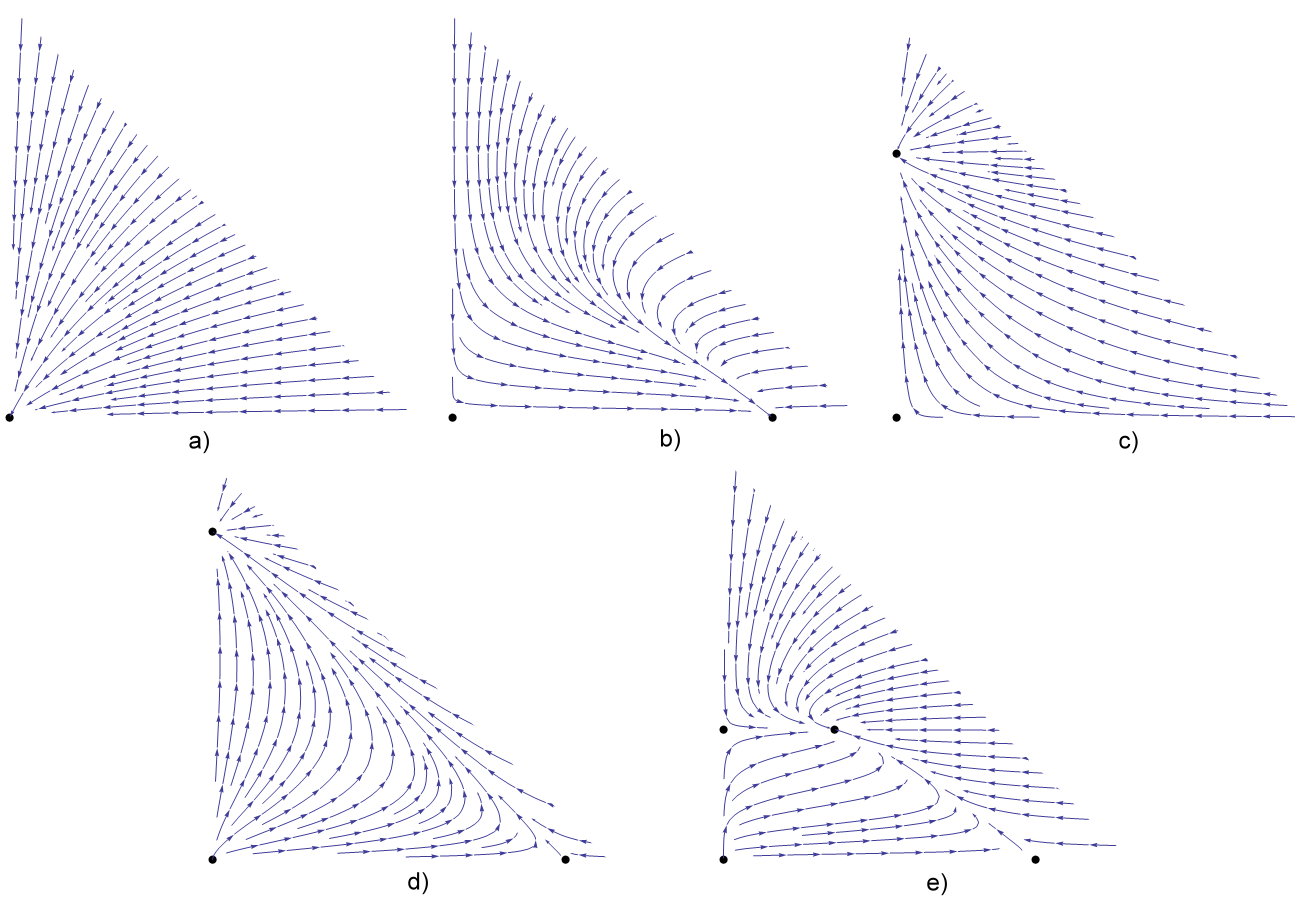A globális attraktor szerkezete a reprodukciós számok függvényében

Eredményeink szerint a betegség kiirtásához az R2 reprodukciós számot kell 1 alá csökkentenünk, ha pedig a parazitafertőzést is teljesen meg szeretnénk szüntetni, akkor az R1 reprodukciós számot is 1 alá kell csökkentenünk. Erre a betegek elkülönítésével, a kezelések nagyobb elterjedésével van lehetőség.  Amennyiben R2>1, akkor a harmadik reprodukciós szám arról dönt, hogy minden parazita fertőzött-e.

A bizonyításnál felhasznált matematikai módszerek: stabilitáselmélet, Ljapunov-függvények, LaSalle-féle invarianciaelv, globális attraktorok, perzisztenciaelmélet. Modellünk realisztikusabbá tételének érdekében további munkánkban a rendszert kibővítettük egy újabb részpopulációval, amelybe azok tartoznak, akiket a parazitáktól már fertőtlenítettek, a betegséget azonban még hordozzák. A rendszer viselkedése hasonló az egyszerűbb modelléhez, az ott alkalmazott technikák azonban bonyolultabb módon, vagy egyáltalán nem alkalmazhatóak, így a bizonyítás további eszközöket (pl. Poincaré–Bendixson-tétel, Dulac-kritérium) igényel.

Hasonlóa eszközöket igényelnek a bizonyítások abban az esetben, ha a betegség okozta halálozást - amely pl. a tífusz és a pestis esetében igen jelentős - is figyelembe vesszük a modellben.

További felmerülő kérdés az az eset, amikor a fogékonyak és a nem fertőző élősködőkkel fertőzöttek, illetve a fogékonyak és a fertőző élősködőkkel fertőzöttek közti átviteli ráta különböző. Ebben az esetben jóval bonyolultabb formulákat kapunk az egyensúlyi helyzetekre és a reprodukciós számokra, emiatt az egyszerűbb modellben alkalmazott Ljapunov-függvényeket itt nem tudjuk alkalmazni. Számos, ektoparaziták okozta betegség néhány naptól két hétig terjedő látens periódussal kezdődik, ami funkcionál-differenciálegyenletes modellek használatát igényli. Jól ismert, hogy számos élősködőt, amelyek a különböző betegségek terjedéséért felelősek, állatok (pl. egerek, patkányok) terjesztenek. Újabb lehetőség a modellünk továbbfejlesztésére, ha ezt a jelenséget is leíró rendszert adunk meg.