Populációdinamika

A matematika történetének egyik legnagyobb és legtermékenyebb alakja, a svájci születésű Leonhard Euler (1707-1783) a matematika valamennyi területén jelentős eredményeket ért el. 1748-ban megjelent Introductio in analysin infinitorum című művében négy populációdinamikai problémát is felvetett. Ezek közül az egyikben azt tesszük fel, hogy a Pn populációra az n-edik évben a egyenlet teljesül, ahol x növekedési ráta valamilyen pozitív szám. Ez azt jelenti, hogy ha egy P0 kezdeti értékből indulunk, akkor az n-edik évben a populáció méretét a
egyenlet adja meg, vagyis a népesség exponenciálisan nő.

Euler négy példája közül az első így szól: Ha egy bizonyos terület népessége évente harmincadával nő, és egy adott időpontban a területnek 100 ezer lakosa volt, tudni szeretnénk, mekkora lesz a lakosság száz év múlva. Az előző képletünkbe behelyettesítve P0 helyére 100000-et, x helyére 1/30-ot, n helyére pedig százat, könnyen megkapjuk a választ (legalábbis ha van számológépünk, Euler idejében ez nyilván nehezebben ment). A példát az 1747-es berlini népszámlálás ihlette, melynek során Berlin lakosságát 107224 főben állapították meg. Euler számításai szerint egy város népessége akár több mint tízszeresére is nőhet egyetlen évszázad alatt - ezt abban az időben London példája is igazolta.

A második probléma még érdekesebb kérdést vet fel: Mivel az Özönvíz után minden ember egy hat főből álló populációból származik, ha feltesszük, hogy kétszáz év után egymillióra nőtt a népesség, tudni szeretnénk az éves növekedési rátát.

Ha megoldjuk a feladatot, azt kapjuk, hogy a növekedése ráta 1/16 körül van, ami egészen realisztikus. A vallásos Euler e példa megoldásával az Özönvíz történetében kételkedőket is igyekezett meggyőzni.  Egyúttal viszont azt is megállapította, hogy ha a növekedés 400 éven át ilyen ütemben halad, akkor a Föld népessége 166 milliárdra nő, ekkora népességet viszont a bolygó képtelen lenne eltartani. Ezt az ötletet fejlesztette tovább kb. fél évszázaddal később az angol Thomas Robert Malthus (1766-1834). Malthus 1798-ban írott Tanulmány a népesedés törvényéről című művében arról írt, hogy a népesség mindig gyorsabban nő a termelésnél, így ugyanannyi élelmiszerre egyre több és több ember jut, vagyis ahelyett, hogy a gazdasági növekedés hatására a jólét a társadalom minden rétegére kiterjedne, ahogy azt a kor jelentős gondolkodói vélték, Malthus szerint egyes társadalmi csoportok éhezésre, nyomorra, betegségre vannak ítélve. Arról, hogy ez a tendencia ne váljon végzetessé, maga a természet gondoskodik a háborúk, a betegségek és a bűn segítségével. Malthus elméleteit nem fordította le matamatikai modellek nyelvére, viszont kikövezte az utat a belga Pierre-François Verhulst (1804-1849) számára. Verhulst 1825-ben szerzett doktori fokozatot, és 1835-ben lett a matematika professzora a brüsszeli egyetemen, abban az évben, mikor honfitársa, Adolphe Quetelet egy publikációjában arról írt, hogy egy populáció nem növekedhet exponenciálisan hosszú időn át a Malthus által is említett akadályok miatt, az akadályok hatását (mechanikai modellek analógiájára) a populáció növekedésének négyzetével arányosnak gondolta. Verhulst valószínűleg látta, hogy ennek az analógiának nem sok alapja van, és a következő egyenletet javasolta: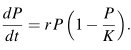Ha P kicsi a K-hoz képest, akkor az egyenlet majdnem megegyezik a dP/dt=rP egyenlettel, amelynek megoldása P(0)*exp(rt), vagyis a megoldás exponenciálisan nő. A növekedési ráta azonban egyre csökken, amint P a K-hoz közelít, sőt, P>K esetén az egyenlet jobb oldala negatív, vagyis a megoldás (a populáció mérete) csökkenni fog. P(0)<K esetén a megoldás folyamatosan növekedve tart a K-hoz, amint t a végtelenbe tart. Verhulst eredményeit összevetette különböző valós adatokkal (Franciaország, Belgium, Essex, Oroszország népességének növekedéséről), és úgy találta, hogy a modell rendkívül jól közelíti a valóságot.

1845-ben újabb populációdinamikai témájú cikket jelentetett meg, amelyben újra foglalkozott a fenit, általa logisztikusnak nevezett egyenlettel. Megállapította, hogy a P(t) megoldásgörbe konvex P(t) < K/2 esetén, és konkáv, ha P(t) > K/2. Azt is megmutatta, hogy a K és r paraméterek hogyan becsülhetők, ha ismerjük a P(t) függvény értékét három különböző időpontban (úgy, hogy a második időpont távolsága egyenlő az első és a harmadik időponttól): ha P0 jelöli a populáció méretét a t1 időpontban, P1 a t=T időpontban, P2 pedig a t=2T időpontban, akkor a következő értékékeket kapjuk:

Verhulst ezeket a becsléseket Belgiumra alkalmazta az 1815-ös, 1830-as és 1845-ös népességgel számolva, és a K=6,584 millió és r=2,62%/év értékeket kapta, és így az egyenletből 1851-re 4,998 milliós, 1900-ra pedig 6,064 milliós népességet jósolt. Franciaországra alkalmazva a K=39,685 millió és r=3,2%/év értékek adódtak.Mivel a két ország népessége már messze meghaladta a Verhulst által számított K eltartóképességet, arra a következtetésre juthatunk, hogy a logisztikus modell legfeljebb néhány évtizedes időszakokra adhat realisztikus eredményeket.

Néhány évvel későbbi művében Verhulst a logisztikus egyenlet helyett a következő differenciálegyenletet vizsgálta:
Az új egyenlettel már K=9,4 milliós becslést kapott az eltartóképességre.

Felhasznált irodalom:
[1] N. Bacaër, A Short History of Mathematical Population Dynamics, Springer, 2011