Populációdinamika

Patrick Holt Leslie 1900-ban született a skóciai Edinburgh közelében. Oxfordban tanult, de orvosi tanulmányait egészségi problémái miatt abba kellett hagynia. Miután néhány évig a patológiai osztályon dolgozott bakteriológusasszisztensként, statisztikával kezdett foglalkozni, és 1935-ben az újonnan létrehozott Bureau of Animal Population kutatóközpontban kezdett dolgozni. A kutatóközpont célja az volt, hogy az állatok - elsősorban rágcsálók - számának fluktuációját vizsgálja. Többek között a kanadai Hudson-öböl Társaság adatai alapján a mezei nyulak, és a rájuk vadászó hiúzok számának vizsgálatával, a szürke mókusnak a vörös mókus kárára történő angliai térnyerésével, valamint az Oxford környéki pockokra vonatkozó adatokkal foglalkoztak. Leslie Lotka emberi populációkra vonatkozó eredményeit alkalmazta a pockokra. 

Leslie 1945-ben jelentette meg híres, On the use of matrices in certain population mathematics című cikkét a Biometrika folyóiratban, amelyben egy állatpopulációban (pl. patkányok) a nőstények számának növekedését modellezi. A populációt K+1 csoportra osztjuk, Pk,n jelöli a k korú nőstények számát az n időpontban (k=1,2,...,K, n=0,1,...). Jelölje fk a k korú nőstények termékenységét, pontosabban az egy nőstényre eső nőstény utódok számát az n és n+1 időpontok között. K a maximális kor nullától különböző termékenységgel. Jelölje sk annak a valószínűségét, hogy egy k korú egyed legalább k+1 idős koráig életben marad. Ekkor a populáció korstruktúráját a következő egyenletek adják meg:

 Mindegyik fk nemnegatív, valamint 0<sk<1 teljesül.A fenti egyenletrendszert rövidebben a

alakban írhatjuk, ahol Pn a (P0,n,...PK,n) oszlopvektor, M pedig a következő négyzetes mátrix:A fenti egyenletrendszer viselkedésének megértésére Leslie alakú, mértani növekvő vagy csökkenő sorozat formájában keresett megoldást, ahol az r szám és a Vvektor teljesítik az MV=rV feltételt. Ekkor r-et az M mátrix sajátértékének, V-t pedig a mátrix sajátvektorának nevezzük. Más szavakkal, a feladat az, hogy olyan V koreloszlást találjunk, amely minden lépésben az r konstanssal szorzódik. Lotka terminológiájával élve az ilyen eloszlásokat stabilnak nevezzük. Az MV=rV egyenletet azalakban is írhatjuk. Az utolsó K egyenletből következik, hogy 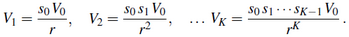Ezt az első egyenletbe behelyettesítve, egyszerűsítve V0-lal, és szorozva r^K-val, Leslie a következő karakterisztikus egyenletet kapta: 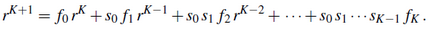Ez egy r-ben K+1-edfokú polinomegyenlet, vagyis K+1 valós vagy komplex gyöke van. Leslie észrevette, hogy csak egy pozitív valós gyök van, jelöljük ezt r1-gyel. A Pn korstruktúravektor minden komponense (r1)^n-hez hasonlóan nő vagy csökken. Ha r1>1, akkor a populáció exponenciálisan nő, ha pedig r1<1, akkor exponenciálisan csökken.  A fenti karakterisztikus egyenletből könnyen látható, hogy az r1>1 feltétel pontosan akkor teljesül, ha az 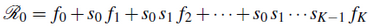képlettel definiált R0 szigorúan nagyobb 1-nél. Vegyük észre, hogy s0s1...sk-1 a legalább k korig való túlélés valószínűsége. Tehát az R0 paraméter az egy nőstény által életes során világra hozott nőnemű utódok átlagos száma. 

Leslie a módszerét egy amerikai kollégája által publikált, a barna patkányra vonatkozó adatokat használva illusztrálta, és az R0=26 értéket kapta. Leslie módszerét ma számos biológus alkalmazza. A számítások napjainkban sokat egyszerűsödtek a számítógépeknek köszönhetően, amelyek segítségével könnyen lehet sajátértékeket és sajátvektorokat, és így az R0 értékét kiszámítani.

A második világháborút követően Leslie más állatfajokra: rovarokra, madarakra alkalmazta módszerét. Sztochasztikus modelleken is dolgozott. 1967-ben vonult nyugdíjba, és 1972-ben hunyt el. 

Felhasznált irodalom:
[1] N. Bacaër, A short history of mathematical population dynamics, Springer. -->